[Tensorflow] Tensorflow卷积理解

Tensorflow convolution

CNN

CNN对于学习深度学习的人来说应该是比较耳熟的名词了.但很多人只是听过,但不知道是什么.

CNN全称是convolutional neural network,可以这么说,只要神经网络里有一层卷积层,就可以称其为CNN.

目前,CNN在物体识别领域使用的非常广泛,比如R-CNN,Faster R-CNN,R-FCN,SSD等很多优秀模型都在使用卷积网络.

所以作为实践者,肯定希望自己用代码去实现这些模型.这里便是对Tensorflow的conv系列方法使用的尝试.

conv2d

因为图像识别应用更加广泛,而且二维更好理解,所以从conv2d方法开始.

函数

conv2d(
    input,
    filter,
    strides,
    padding,
    use_cudnn_on_gpu=True,
    data_format='NHWC',
    name=None
)

计算一个二维的卷积.传入四维的input,该Tensor的形状为[batch, in_height, in_width, in_channels].还要传入一个形状为[filter_height, filter_width, in_channels, out_channels]的四维卷积核.
这个方法做了如下操作:

1. 将卷积核压成形状为[filter_height * filter_width * in_channels, output_channels]的二维矩阵
2. 从输入Tensor提取图像patches(其实就是把每个channel提出来),生成一个虚拟的Tensor[batch, out_height, out_width, filter_height * filter_width * in_channels]
3. 对每个patch,把每个图像patch向量右乘卷积核矩阵

整体来讲,在默认的NHWC格式下,

output[b, i, j, k] = sum_{di, dj, q} input[b, strides[1] * i + di, strides[2] * j + dj, q] * filter[di, dj, q, k]

这里strides[0] = strides[3] = 1.对于常见的纵横方向上等量步长,有strides = [1, stride, stride, 1]

参数

• input:是一个四维Tensor,数据类型必须是half或float32.每层维度解释是通过data_format决定的.
• filter:也是一个四维Tensor,数据类型要和input一致,形状为[filter_height, filter_width, in_channels, out_channels]
• strides:是一个ints列表.长度为4的一维tensor.是在input每个维度上滑动窗口时每次滑动的步长.其维度顺序也是由data_format决定
• padding: 有两个string类型值,”SAME”, “VALID”.涉及到卷积核移动范围.
• use_cudnn_on_gpu: bool值,默认True.使用GPU计算的选项.
• data_format: 两种string类型的值: NHWC, NCHW. 默认NHWC. 指定输入输出数据维度的意义. NHWC的数据顺序为: [batch, height, width, channels].NCHW数据顺序为: [batch, channels, height, width].
• name: 该方法的名字,可选参数,TensorBoard会用到.

返回值

和input一样形状的Tensor

示例

import tensorflow as tf

二维卷积比较多的用在图像数据处理上.我们假设有一个3x3,1通道的图片:

input_img = tf.constant([[[[1], [2], [3]],
                          [[4], [5], [6]],
                          [[7], [8], [9]]]], tf.float32, [1, 3, 3, 1])

然后再设计一个1x1的卷积核,按照步长为1的长度在图像上滑动,计算卷积.

conv_filter1 = tf.constant([[[[2]]]], tf.float32, [1, 1, 1, 1])
op1 = tf.nn.conv2d(input_img, conv_filter1, strides=[1, 1, 1, 1], padding='VALID')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(op1)

运行结果：

[[[[  2.]
   [  4.]
   [  6.]]

  [[  8.]
   [ 10.]
   [ 12.]]

  [[ 14.]
   [ 16.]
   [ 18.]]]]

看到结果,是图像每个像素和卷积核相乘. 我们再看看多通道的图像,把原来的图片变成5个通道.

input_img2 = tf.constant([[[[1, 1, 1, 1, 1],
                            [2, 2, 2, 2, 2],
                            [3, 3, 3, 3, 3]],
                           [[4, 4, 4, 4, 4],
                            [5, 5, 5, 5, 5],
                            [6, 6, 6, 6, 6]],
                           [[7, 7, 7, 7, 7],
                            [8, 8, 8, 8, 8],
                            [9, 9, 9, 9, 9]]]], tf.float32, [1, 3, 3, 5])

因为图像通道变为5,卷积核的输入通道也要填为5.卷积核的输出通道我们先用1通道:

conv_filter2 = tf.constant([[[[2]]]], tf.float32, [1, 1, 5, 1])
op2 = tf.nn.conv2d(input_img2, conv_filter2, strides=[1, 1, 1, 1], padding='VALID')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(op2)

运行结果：

[[[[ 10.]
   [ 20.]
   [ 30.]]

  [[ 40.]
   [ 50.]
   [ 60.]]

  [[ 70.]
   [ 80.]
   [ 90.]]]]

通过运行结果,不难猜出,卷积核对5个通道都进行了计算,然后因为输出为1通道,所以把这5层叠加起来输出.

自然地,我们也可以推测卷积核输出5通道的话,应该是分5个通道的结果.尝试一下:

conv_filter3 = tf.constant([[[[2]]]], tf.float32, [1, 1, 5, 5])
op3 = tf.nn.conv2d(input_img2, conv_filter3, strides=[1, 1, 1, 1], padding='VALID')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(op3)

运行结果：

[[[[ 10.  10.  10.  10.  10.]
   [ 20.  20.  20.  20.  20.]
   [ 30.  30.  30.  30.  30.]]

  [[ 40.  40.  40.  40.  40.]
   [ 50.  50.  50.  50.  50.]
   [ 60.  60.  60.  60.  60.]]

  [[ 70.  70.  70.  70.  70.]
   [ 80.  80.  80.  80.  80.]
   [ 90.  90.  90.  90.  90.]]]]

结果的确如我们所料.

现在我们放大卷积核,1x1的卷积核看不出计算方式,我们换2x2的试试看.运行代码前可以先想想结果,2x2的核在3x3的图像上滑动,滑动步长为1,那么结果应该也是2x2的.

conv_filter4 = tf.constant([[[[2]], [[4]]], [[[3]], [[1]]]], tf.float32, [2, 2, 1, 1])
op4 = tf.nn.conv2d(input_img, conv_filter4, strides=[1, 1, 1, 1], padding='VALID')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(op4)

运行结果：

[[[[ 27.]
   [ 37.]]

  [[ 57.]
   [ 67.]]]]

上面我们使用了

2 4 
3 1

的卷积核在原图

1 2 3
4 5 6 
7 8 9

上滑动

第一个值的计算是1x2+2x4+4x3+5x1=27.

然后卷积核向右移动一格,继续计算: 2x2+3x4+5x3+6x1=37.

前两行遍历完卷积核从第2行开始,继续向右遍历.得到最后的结果.

这里有个卷积工作的参考图: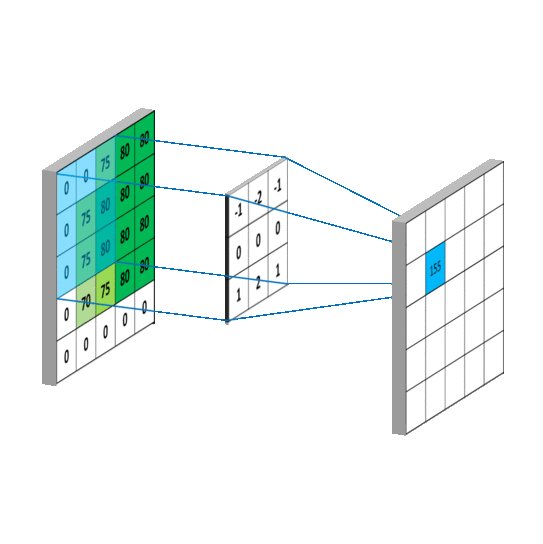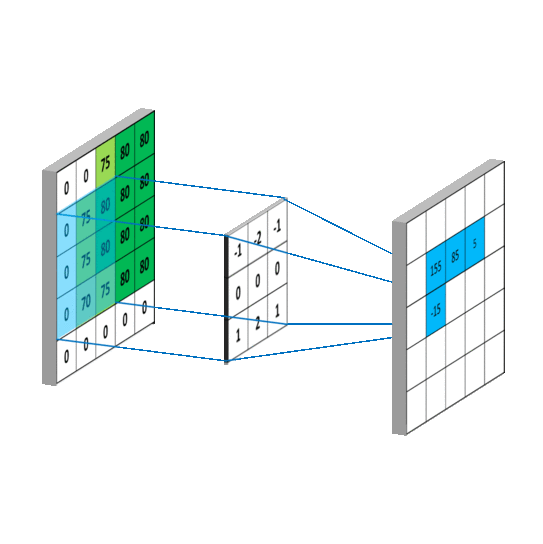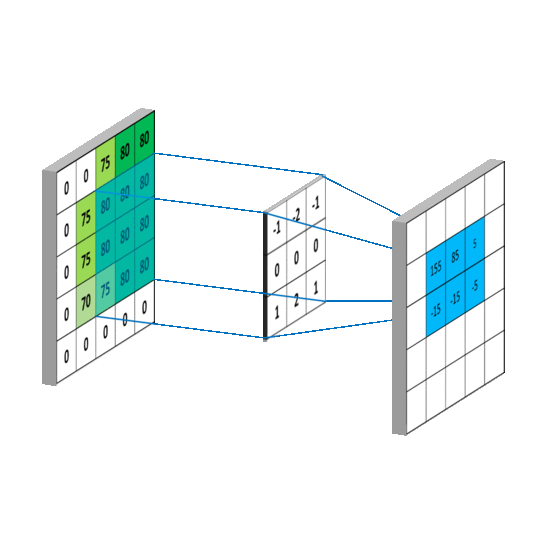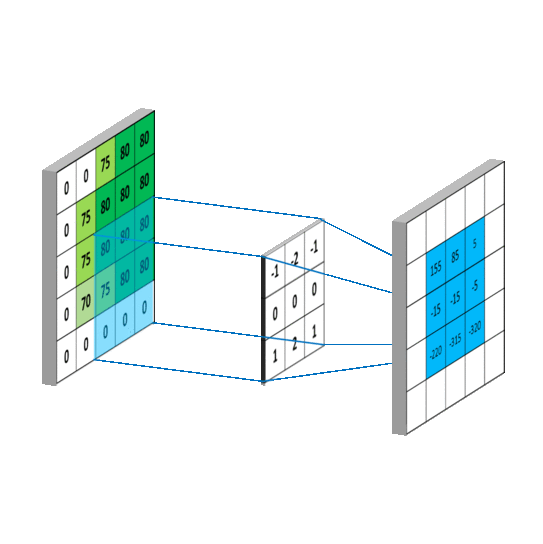

图片出处https://mlnotebook.github.io/post/CNN1/

有了前面的了解,可以聊一聊padding参数了.前面的例子,我们的卷积核都是在图片范围内移动的,永远不会超出图像的边缘.

这样有一个问题就是如果卷积核size很大,比如用3x3的,那么我们3x3的图像就只能输出一个1x1的值.这个值可能代表了图片中心的一个特征,而图像边缘的信息就被弱化了.再假如我们这个图像就是个空心圆,特征都在边缘,那这个卷积核就不能够很好地体现出图片的特征.

所以为了解决边缘问题,我们会适当地拓展图像,让卷积核可以在原始尺寸外移动.

但卷积核终究是要计算的,移动到外面和谁去相乘呢?一般做法就是填0,就好像上面的gif图,图片本身是4x4的,但在左侧和底侧都填满了0,让卷积核可以多一些输出.实际中,往哪个方向拓展图片,填0还是其他数字都是根据情况选择的.

上面是我个人的理解.我们用Tensorflow看看他们是怎么做的.我们把padding参数改成SAME:

conv_filter5 = tf.constant([[[[2]], [[4]]], [[[3]], [[1]]]], tf.float32, [2, 2, 1, 1])
op5 = tf.nn.conv2d(input_img, conv_filter5, strides=[1, 1, 1, 1], padding='SAME')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(op5)

运行结果：

[[[[ 27.]
   [ 37.]
   [ 24.]]

  [[ 57.]
   [ 67.]
   [ 39.]]

  [[ 46.]
   [ 52.]
   [ 18.]]]]

从结果上看,原本是

27 37
57 67

的结果变成了

27 37 24
57 67 39
46 52 18

实际上Tensorflow对padding有一套自己的计算方式:

为了方便理解,我们分水平方向和垂直方向.(源码是直接使用Size)

我们的情况是:input是3x3, filter是2x2, Stride是1, output是WxH

output_size = (input_size + stride -1) / stride >> W=(3+1-1)/1=3

需要添加的padding大小为

pad_need = max(0, (output_size - 1) * stride + filter_size - input_size) = max(0, (3-1)x1+2-3)=1

往图片左边添加的pad_left = pad_need / 2 = 1 / 2 = 0

往图片右边添加的pad_right = pad_need - pad_left = 1 - 0 = 1

纵向同样计算方式.所以最后的图像变成

1 2 3 0
4 5 6 0
7 8 9 0
0 0 0 0

最后再计算卷积,得到的结果就是上面运行的结果.

源码在/tensorflow/tensorflow/core/framework/common_shape_fns.cc

最后再看看步长stride

默认NHWC格式下,stride是[batch, height, width, channels],在二维情况下,height对应纵向移动步长,width对应水平移动步长.一般情况,二维stride写成[1, stride, stride,1]的形式.

我们使用1x1的卷积核对3x3的图片以步长为2处理:

conv_filter6 = tf.constant([[[[2]]]], tf.float32, [1, 1, 1, 1])
op6 = tf.nn.conv2d(input_img, conv_filter6, strides=[1, 2, 2, 1], padding='VALID')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(op6)

运行结果：

[[[[  2.]
   [  6.]]

  [[ 14.]
   [ 18.]]]]

结果是原来3x3的四个角.很容易理解.再试试不同方向不同的stride

op7 = tf.nn.conv2d(input_img, conv_filter6, strides=[1, 2, 1, 1], padding='SAME')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print sess.run(op7)

运行结果：

[[[[  2.]
   [  4.]
   [  6.]]

  [[ 14.]
   [ 16.]
   [ 18.]]]]

横向移动为1,纵向为2,结果就是2x3.

至此,Tensorflow二维的卷积应该就比较清楚了.

conv1d

有了2d卷积的理解,看1d应该更容易.对一维来讲,卷积就是对一条线一小段一小段地叠加.这个我会结合DeepLearning这本书上的卷积章节做一些整理.

函数

conv1d(
    value,
    filters,
    stride,
    padding,
    use_cudnn_on_gpu=None,
    data_format=None,
    name=None
)

参数

从二维卷积降到一维,我们的数据自然也从四维降到三维.

所以

• input的形状就变成[batch, in_width, in_channels]
• filter的形状变为[filter_width, in_channels, out_channels]
• stride变成一个整形数字

实际上,一维的卷积方法在运行时,会把数据增加一维,然后使用conv2d方法计算.

变换过程是:

• [batch, in_width, in_channels]->[batch, 1, in_width, in_channels]
• [filter_width, in_channels, out_channels]->[1, filter_width, in_channels, out_channels]

返回值

当然,计算结果是升维的结果,返回时需要做一次降维.最终返回结果是[batch, out_width, out_channels]

conv3d

函数

conv3d(
    input,
    filter,
    strides,
    padding,
    data_format='NDHWC',
    name=None
)

In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product.

Our Conv3D implements a form of cross-correlation.

参数

主要是增加一个维度

• input:[batch, in_depth, in_height, in_width, in_channels]
• filter:[filter_depth, filter_height, filter_width, in_channels, out_channels]

返回值

同input

conv2d_backprop_filter

根据filter计算卷积的梯度

conv2d_backprop_input

根据input计算卷积的梯度

conv2d_transpose

这个方法有时被成为反卷积,实际上更准确的是对conv2d的转置.

参考

Tensorflow中卷积的padding操作

tf.nn.conv2d